外部索引

二元搜尋樹（Binary Search Tree）應用在外部索引有不同的變型

2-3 Trees

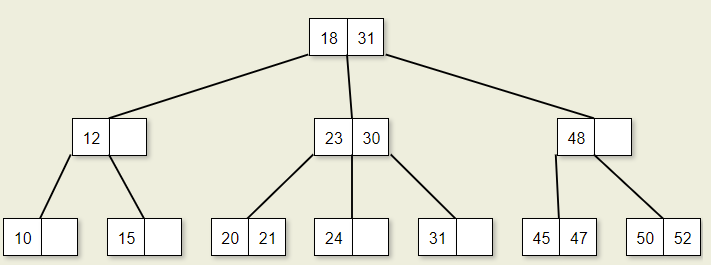
/** 2-3 tree node implementation */
class TTNode<Key extends Comparable<? super Key>,E> {
private E lval; // The left record
private Key lkey; // The node’s left key
private E rval; // The right record
private Key rkey; // The node’s right key
private TTNode<Key,E> left; // Pointer to left child
private TTNode<Key,E> center; // Pointer to middle child
private TTNode<Key,E> right; // Pointer to right child
public TTNode() { center = left = right = null; }
public TTNode(Key lk, E lv, Key rk, E rv,
TTNode<Key,E> p1, TTNode<Key,E> p2,
TTNode<Key,E> p3) {
    lkey = lk; rkey = rk;
    lval = lv; rval = rv;
    left = p1; center = p2; right = p3;
}
public boolean isLeaf() { return left == null; }
public TTNode<Key,E> lchild() { return left; }
public TTNode<Key,E> rchild() { return right; }
public TTNode<Key,E> cchild() { return center; }
public Key lkey() { return lkey; } // Left key
public E lval() { return lval; } // Left value
public Key rkey() { return rkey; } // Right key
public E rval() { return rval; } // Right value
public void setLeft(Key k, E e) { lkey = k; lval = e; }
public void setRight(Key k, E e) { rkey = k; rval = e; }
public void setLeftChild(TTNode<Key,E> it) { left = it; }
public void setCenterChild(TTNode<Key,E> it)
{ center = it; }
public void setRightChild(TTNode<Key,E> it)
{ right = it; }

B-Tree

B樹（B-tree）是一種自平衡(AVL)的樹，能夠保持數據有序。這種資料結構能夠讓查找數據、順序訪問、插入數據及刪除的動作，都在對數時間內完成。B樹，概括來說是一個一般化的二元搜尋樹（binary search tree），可以擁有多於2個子節點。與自平衡二元搜尋樹不同，B樹為系統大塊數據的讀寫操作做了優化。B樹減少定位記錄時所經歷的中間過程，從而加快存取速度。B樹這種資料結構可以用來描述外部存儲。這種資料結構常被應用在資料庫和文件系統的實現上。

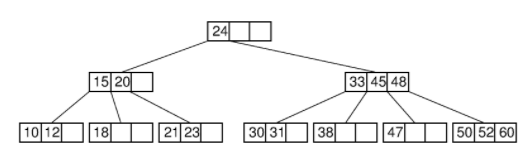
// Template

B+Tree

B+ 樹的特點是能夠保持資料穩定有序，其插入與修改擁有較穩定的對數時間複雜度。B+ 樹元素自底向上插入，這與二元樹恰好相反。

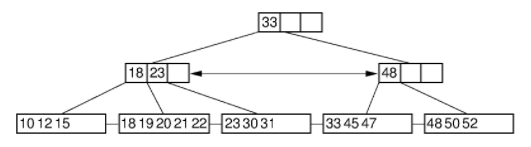
B+Tree尋找

尋找以典型的方式進行，類似於二元搜尋樹。起始於根節點，自頂向下遍歷樹，選擇其分離值在要尋找值的任意一邊的子指標。在節點內部典型的使用是二分尋找來確定這個位置。

B+Tree插入

節點要處於違規狀態，它必須包含在可接受範圍之外數目的元素。首先，尋找要插入其中的節點的位置。接著把值插入這個節點中。如果沒有節點處於違規狀態則處理結束。如果某個節點有過多元素，則把它分裂為兩個節點，每個都有最小數目的元素。在樹上遞迴向上繼續這個處理直到到達根節點，如果根節點被分裂，則建立一個新根節點。為了使它工作，元素的最小和最大數目典型的必須選擇為使最小數不小於最大數的一半。

B+Tree刪除

首先，尋找要刪除的值。接著從包含它的節點中刪除這個值。如果沒有節點處於違規狀態則處理結束。如果節點處於違規狀態則有兩種可能情況：它的兄弟節點，就是同一個父節點的子節點，可以把一個或多個它的子節點轉移到當前節點，而把它返回為合法狀態。如果是這樣，在更改父節點和兩個兄弟節點的分離值之後處理結束。它的兄弟節點由於處在低邊界上而沒有額外的子節點。在這種情況下把兩個兄弟節點合併到一個單一的節點中，而且我們遞迴到父節點上，因為它被刪除了一個子節點。持續這個處理直到當前節點是合法狀態或者到達根節點，在其上根節點的子節點被合併而且合併後的節點成為新的根節點。

/** Interface for B+ Tree nodes */
public interface BPNode<Key,E> {
  public boolean isLeaf();
  public int numrecs();
  public Key[] keys();
}

Chapter12 外部索引