106-1作業

課本Data Structures & Algorithm Analysis by Clifford A. Shaffer https://people.cs.vt.edu/shaffer/Book/

作業一(106-1-Assignment1)

• P20: 1.3, 1.11
• P47 2.11, 2.21

1.3 Define an ADT for character strings. Your ADT should consist of typical functions that can be performed on strings, with each function defined in terms of its input and output. Then define two different physical representations for strings.

Ans: https://en.wikipedia.org/wiki/Comparison_of_programming_languages_(string_functions) http://web.mit.edu/6.005/www/fa14/classes/08-abstract-data-types/ 參考P.96

/** Character strings ADT */
public class MyString { 
    public int length();
    public char charAt(int i);
    public MyString substring (int start, int end);
}

1.11 Consider the design for a spelling checker program meant to run on a home computer. The spelling checker should be able to handle quickly a document of less than twenty pages. Assume that the spelling checker comes with a dictionary of about 20,000 words. What primitive operations must be implemented on the dictionary, and what is a reasonable time constraint for each operation?

Ans: http://www.husseinsspace.com/teaching/vt/1999/cs2604/homework/hw1.htm (1) primitive operations must be implemented on the dictionary (2) time constraint

1. Build-dictionary (taking a maximum of, say, 10 seconds) - creates a representation of the dictionary in main memory.

   • Includes 20000 Insert-into-dictionary operations, each of which will need to take an average of 0.0005 seconds.
   • Insert-into-dictionary may be preceded by Read-word-from-dictionary, which sequentially reads in a dictionary word from the ASCII listing in secondary storage. The time taken for this must be incorporated into the 0.0005 seconds (if we assume that I/O operations take the most time then the whole 0.0005 seconds would be allocated to this operation, and the previous one would require a relatively negligible amount of time)

2. Find-word-in-dictionary - checks if a particular word is in the dictionary. Suppose the maximum reasonable time to search 20 pages is 20 seconds. This means that each page must take at most 1 second. Assuming 66 lines per page and 14 words per line, this implies a time constraint of approximately 0.001 second per search operation.

   • This could be preceded by Read-word-from-document, which will take a negligible amount of time if we assume the document is in main memory.

2.11 Here is a simple recursive function to compute the Fibonacci sequence:

/** Recursively generate and return the n’th Fibonacci
number */
static long fibr(int n) {
    // fibr(91) is the largest value that fits in a long
    assert (n > 0) && (n <= 91) : "n out of range";
    if ((n == 1) || (n == 2)) return 1; // Base case
        return fibr(n-1) + fibr(n-2); // Recursive call
}

This algorithm turns out to be very slow, calling Fibr a total of Fib(n) times. Contrast this with the following iterative algorithm:

/** Iteratively generate and return the n’th Fibonacci number */
static long fibi(int n){
    // fibr(91) is the largest value that fits in a long assert (n > 0) && (n <= 91) : "n out of range";
    long curr, prev, past;
    if ((n == 1) || (n == 2)) return 1;
    curr = prev = 1; // curr holds current Fib value
    for (int i=3; i<=n; i++) { // Compute next value
        past = prev; // past holds fibi(i-2)
        prev = curr; // prev holds fibi(i-1)
        curr = past + prev; // curr now holds fibi(i)
    }
    return curr;
}

Function Fibi executes the for loop n−2 times. (a) Which version is easier to understand? Why? (b) Explain why Fibr is so much slower than Fibi

Ans: 費氏數列的定義是$f(n)=f(n-1)+f(n-2)$ (a) fibr() (b) $fibr(n)=O(1.618^n)$ $fibi(n)=O(n)$

2.21 Explain why $\sum_{i=1}^{n} i = sum_{i=1}^{n} (n-i+1)=sum_{i=0}^{n-1}(n-i)$

Ans:

1. 數學規納法 Proof by Mathematical Induction Base case $n=1$ $\sum_{i=1}^{1} i =1=sum_{i=1}^{1} (n-i+1)$ 成立

Inductive hypothesis: 令$n=k$ $\sum_{i=1}^{k} i =sum_{i=1}^{k} (k-i+1)$ 成立

Inductive step: 則當$n=k+1$時 $\sum_{i=1}^{k+1} i = sum_{i=1}^{k} i +(k+1)=sum_{i=1}^{k} (k-i+1)+(k+1) = sum_{i=1}^{k+1} (k+1-i+1)$ $\sum_{i=1}^{n} i = sum_{i=1}^{n}(n-i+1)$

1. 直證式 Direct Proof

令$j=i-1$

$\sum_{i=1}^{n} (n-i+1)=sum_{i=1}^{n}(n-(i-1))=sum_{j=0}^{n} (n-j)=sum_{i=0}^{n-1}(n-i)$

作業二(106-1-Assignment2)

4.7 Write a function to merge two linked lists. The input lists have their elements in sorted order, from lowest to highest. The output list should also be sorted from lowest to highest. Your algorithm should run in linear time on the length of the output list. Ans:

MergeTwoList(List A, List B, List C){
    int x=0, y=0, z;
    for(z=0; z < length(A)+length(B); z++){
        if (x==length(A)){//A沒了
            C[z]=B[y++];
        }else if(y==length(B)){ //B沒了 
            C[z]=A[x++];
        }else if(A[x] <B[y]){
            C[z]=A[x++];
        }else{
            C[z]=B[y++];
        }
    }
}

4.16 Re-implement function fibr from Exercise 2.11, using a stack to replace the recursive call as described in Section 4.2.4. Ans:

fib(x){
  tot = 0
  stack = [x]
  while (stack is not empty){
    a = stack.pop()
    if (a ==0 || a==1){
        tot += 1;
    }else{
         stack.push(a - 1);
         stack.push(a - 2);
    }
   }
   return tot
}

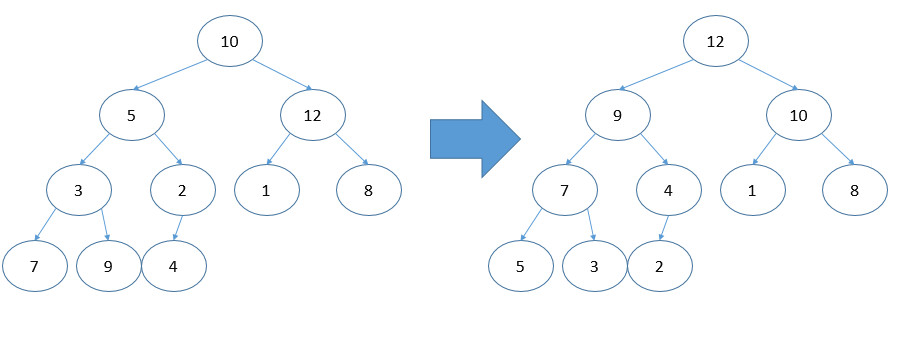
5.25 Show the max-heap that results from running buildHeap on the following values stored in an array: 10 5 12 3 2 1 8 7 9 4 Ans:

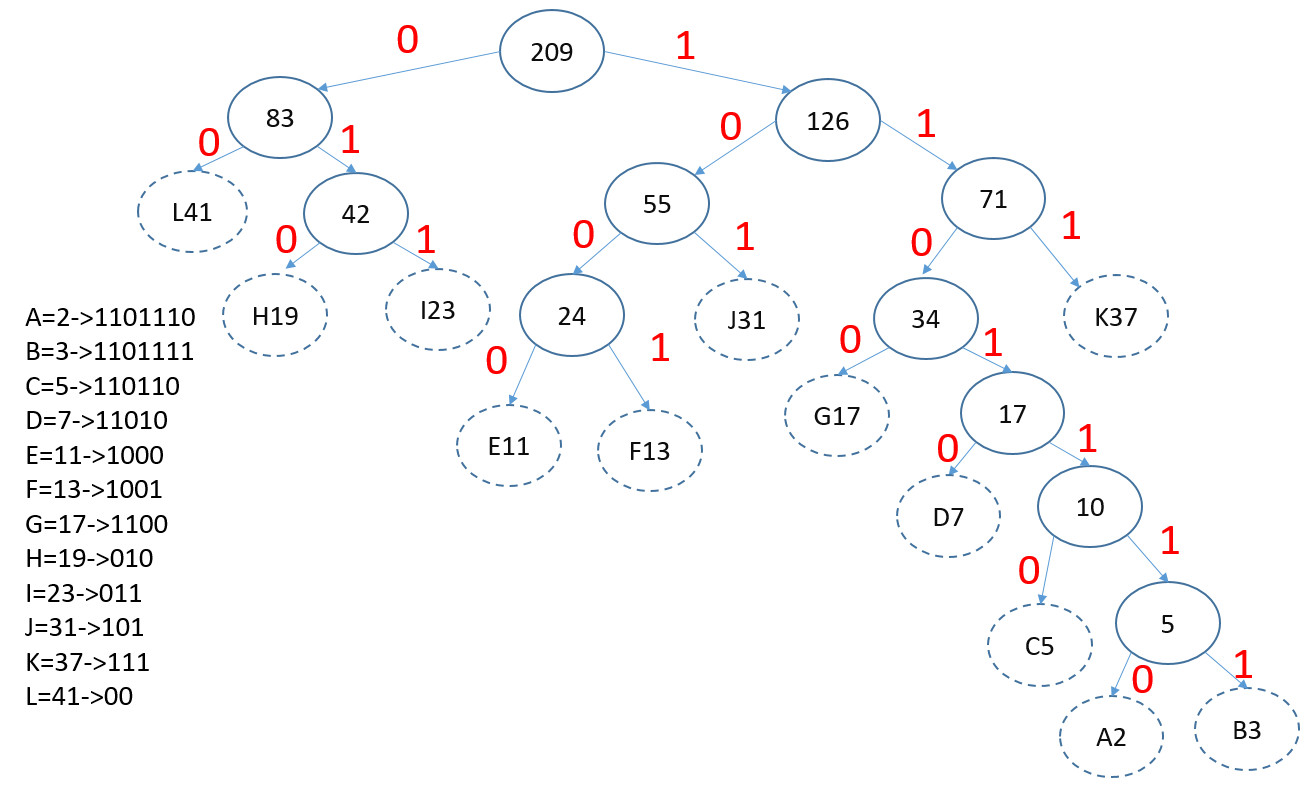
5.28 Build the Huffman coding tree and determine the codes for the following set of letters and weights: Ans:

What is the expected length in bits of a message containing n characters for this frequency distribution?

作業三(106-1-Assignment3)

import java.io.*;
import java.util.*;
public class Ex2Class {

    public static void main(String[] args) {
        //generate 1~6 random numbers
        int num, i, j;
        int[] bin = new int[3000];
        int[] ans = new int[100];
        int bin_length = 3000;
        int select;
        for (i=0; i<bin_length; i++){
            bin[i] = i+2001;
        }
        /* New a random-number generator object */
        Random random = new Random();
        for (i=0; i<100; i++){
            select = (random.nextInt()& Integer.MAX_VALUE)%bin_length;
            ans[i] = bin[select];
        }

        for (i=0; i<100; i++){
            System.out.printf("%5d ", ans[i]);
        }
    }
}

java

作業四(106-1-Assignment4)